Question

Given the function f\left(x\right)=-3x+6f(x)=−3x+6 with a domain of [-2, 7), identify the range of the function using same notation.

Answer 1

The range of the function is represented by
`Ran\{f(x)\} = (-15, 12]`.

Explanation:

Let be
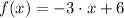`f(x) = -3\cdot x + 6`, for
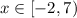`x \in [-2,7)`. As we notice that
`f(x)` is an inyective function, that is, the inexistence of two or more domain element with the same image, with a monotone behavior, we can obtain the bounds of the range of the function by evaluating the expression:

Lower bound (
`x = -2`)

`f(-2) = -3\cdot (-2)+6`

`f(-2) = 12`

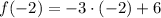
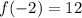
Upper bound (
`x = 7`)

`f(7) = -3\cdot (7)+6`

`f(7) = -15`

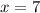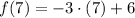
The range of the function is represented by
`Ran\{f(x)\} = (-15, 12]`