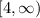Answer:
Function
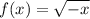 has domain
has domain
![(-\infty ,0]](https://img.qammunity.org/2021/formulas/mathematics/college/1ez7zkjkb4huytts7og6krgyyx4papf40u.png)
Function
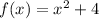 has range
has range
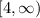
Explanation:
Domain of the function
 refers to the values of
refers to the values of
 and the range refers to the values that the function
and the range refers to the values that the function
 takes for various values of
takes for various values of
 .
.
Consider a function
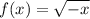
As value within the square root is non-negative.
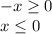
So, domain is
![(-\infty ,0]](https://img.qammunity.org/2021/formulas/mathematics/college/1ez7zkjkb4huytts7og6krgyyx4papf40u.png)
Now, consider a function
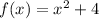
Clearly,
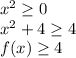
So,
range of
 is
is