Given:
The distance between the two points (11, 1) and (x, 17) is 20.
To find:
The possible values of x.
Solution:
Distance formula is:

Using this formula, the distance between (11, 1) and (x, 17) is


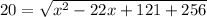
Taking square on both sides.
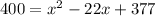
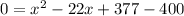
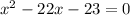
Splitting the middle term, we get
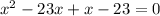
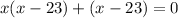
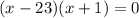
Using zero product property, we get
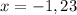
Therefore, the possible values of x are -1 and 23.