Question

The area of a rectangle is 42ft^2, and the length of the rectangle is 11 less than three times the width. Find the dimensions of the rectangle.

Answer 1

7 ft ×6 ft

Explanation:

Area of rectangle= length ×width

Let the length and width of the rectangle be L and W ft respectively.

Form 2 equations using the given information:

LW= 42 -----(1)

L= 3W -11 -----(2)

Substitute (2) into (1):

(3W -11)(W)= 42

Expand:

3W² -11W= 42

3W² -11W -42= 0

`\boxed{x = \frac{ - b± \sqrt{ {b}^(2) - 4ac } }{2a} }`

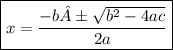
Applying quadratic formula:

`W= \frac{ - ( - 11)± \sqrt{( - 11) {}^(2) - 4(3)( - 42) } }{2(3)}`

`W= ( 11± √(625 ) )/(6)`

`W= ( 11± 25)/(6)`

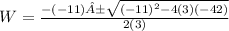
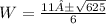
W= 6 or W=
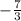`- (7)/(3)` (reject)

Substitute W= 6 into (1):

L(6)= 42

L= 42 ÷6

L= 7

Thus the dimensions of the rectangle is 7 ft ×6 ft.