Question

Given that ‘z’ is in set of complex number and ‘a’ is any real numbers. Solve the trigonometric equation sin(z) = a for all general solutions.

Answer 1

We are given with:

`{\quad \qquad \longrightarrow \sin (z)={\sf a}\:,\:z\in \mathbb{C}}`

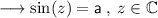
Recall the identity what we have for the sine function of complex numbers

• 
  `{\boxed{\bf{\sin (z)=(e^(\iota z)-e^(-\iota z))/(2\iota)}}}`

Put the values to thus obtain:

`{:\implies \quad \sf (e^(\iota z)-e^(-\iota z))/(2\iota)=a}`

`{:\implies \quad \sf e^(\iota z)-e^(-\iota z)=2a\iota}`

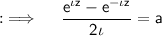
Multiply both sides by
`{\sf e^(\iota z)}`

`{:\implies \quad \sf e^(\iota z)\cdot e^(\iota z)-e^(-\iota z)\cdot e^(\iota z)=2a\iota e^(\iota z)}`

`{:\implies \quad \sf (e^(\iota z))^(2)-2a\iota e^(\iota z)-1=0}`

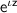
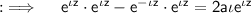
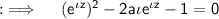
Put x =
`{\sf e^(\iota z)}`:

`{:\implies \quad \sf x^(2)-2a\iota x-1=0}`

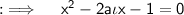
Find the discriminant, here D will be, D = (-2ai)² - 4 × 1 × (-1) = 4 - 4a² = 4(1-a²)

Now, By quadratic formula:

`{:\implies \quad \sf x=\frac{-(-2a\iota)\pm \sqrt{4(1-a^(2))}}{2}}`

`{:\implies \quad \sf x=\frac{a\iota \pm \sqrt{1-a^(2)}}{2}}`

`{:\implies \quad \sf e^(\iota z)=\frac{a\iota \pm \sqrt{1-a^(2)}}{2}}`

`{:\implies \quad \sf \iota z=log\bigg(\frac{a\iota \pm \sqrt{1-a^(2)}}{2}\bigg)}`

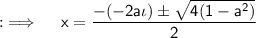
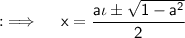
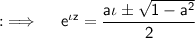
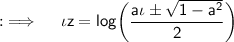
Using the formula for logarithms, we have:

`{:\implies \quad \sf \iota z=log(a\iota \pm \sqrt{1-a^(2)})-log(2)}`

`{:\implies \quad \sf z=(1)/(\iota)log(a\iota \pm \sqrt{1-a^(2)})-(1)/(\iota)log(2)}`

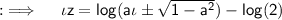
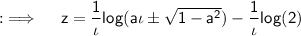
The sine function is periodic on 2πn and zero on (π/2), and the logarithmic expression becomes undefined for all ia±√(1-a²) < 0, so we will take modulus of it

`{:\implies \quad \boxed{\bf{z=(1)/(\iota)log\bigg|a\iota \pm \sqrt{1-a^(2)}\bigg|-(1)/(\iota)log(2)+(\pi)/(2)+2\pi n\:\:\forall \:n\in \mathbb{Z}}}}`

Answer 2

Recall that for all
`z\in\Bbb C`,

`\sin(z) = (e^(iz) - e^(-iz))/(2i)`

so that

`\sin(z) = a \iff e^(iz) - e^(-iz) = 2ia`

Multiply both sides by
`e^(iz)` to get a quadratic equation,

`e^(2iz) - 2iae^(iz) - 1 = 0`

Solve for
`e^(iz)`. By completing the square,

`e^(2iz) - 2ia e^(iz) + i^2a^2 = 1 + i^2a^2`

`\left(e^(iz) - ia\right)^2 = 1 - a^2`

`e^(iz) - ia = \pm √(1-a^2)`

`e^(iz) = ia \pm √(1-a^2)`

`iz = \log\left(ia \pm √(1-a^2)\right)`

`iz = \ln\left|ia \pm √(1-a^2)\right| + i \left(\arg\left(ia \pm √(1-a^2)\right) + 2\pi n\right)`

`\boxedz = -i \ln\left`

where n is any integer.