Answer:
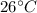
Step-by-step explanation:
Given that the temperature of
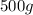 of water and
of water and
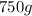 of water are
of water are
at
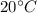 and
and
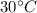 respectively.
respectively.
Let
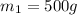 ,
,
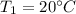
and
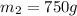 ,
,
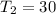 .
.
The specific heat capacity of water is,
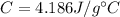 .
.
Let the final temperature of the mixture be
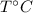 .
.
As there is no energy loss, so, the energy loss by the water at higher temperature, i.e.
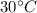 , will be equal to the energy gain by the water at lower temperature, i.e.
, will be equal to the energy gain by the water at lower temperature, i.e.
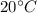 .
.
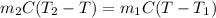
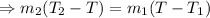 [ both sides divided by
[ both sides divided by
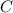 ]
]
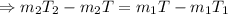
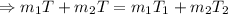
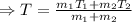
Now, putting the given value in the above equation, we have
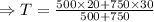
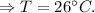
Hence, the temperature of the mixture will be
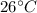 .
.