Question

Trouble finding arclength calc 2

y=3-x^2, 0<=x<=
`√(3)/2`

i determine that the derivative of the y function is -2x and using the arc length formula i get: (a = √3)/2, b=0)

`\int\limits^a_b {√(1+4x^2) } \, dx`
now this is where I get stuck, are we suppose to use u sub somehow? If so, I get u=1+4x^2 and du=4x dx but how to I implement du when it has 4x? please show steps on how to do this

Answer 1

The arc-length is about 1.1953.

Explanation:

We are given the equation:

`y=3-x^2`

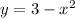
And we want to find the length of its arc from:

`0\leq x\leq \sqrt3/2`

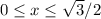
Recall that arc-length is given by the formula:

`\displaystyle S = \int_a^b \sqrt{1+ \left((dy)/(dx)\right)^2}\, dx`

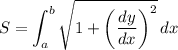
By differentiating and substituting into the arc-length formula, we will acquire:

`\displaystyle S=\int\limits^(√(3)/2)_0 {√(1+4x^2) \, dx`

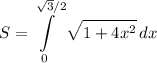
To evaluate, we can use trigonometric substitution. Note that:

`\displaystyle S=\int\limits^\sqrt3/2}_0 {√((1)^2+(2x)^2) \, dx`

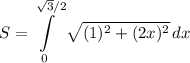
Since this is in the form a² + u², we will make the substitution u = atan(θ).

In this case, a = 1 and u = 2x. Thus:

`\displaystyle 2x = \tan \theta`

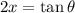
Differentiating both sides with respect to x:

`\displaystyle 2\, dx = \sec^2 \theta \, d\theta`

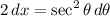
So:

`\displaystyle dx = (1)/(2)\sec^2 \theta \, d\theta`

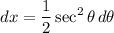
Additionally, we must rewrite our bounds. Hence:

`\displaystyle 2(0) = \tan \theta \Rightarrow \theta = 0`

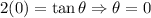
And:

`\displaystyle 2\left((√(3))/(2)\right) = \tan\theta \Rightarrow \theta = (\pi)/(3)`

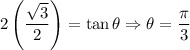
Thus:

`\displaystyle S = \int_(0)^(\pi /3)√(1+(\tan\theta)^2)\cdot (1)/(2)\sec^2\theta\, d\theta`

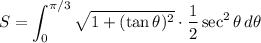
Simplify:

`\displaystyle S = (1)/(2)\int_(0)^(\pi /3)√(1+\tan^2\theta) \cdot \sec^2\theta d\theta`

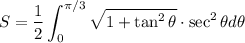
Using trigonometric identities:

`\displaystyle S = (1)/(2)\int_(0)^(\pi /3)√((\sec^2\theta)) \cdot \sec^2\theta d\theta`

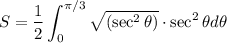
Simplify:

`\displaystyle S = (1)/(2)\int_(0)^(\pi /3) \sec^3\theta \, d\theta`

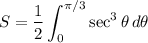
We can apply the reduction formula:

`\displaystyle \int \sec^nu \, du = (\sec^(n-2)u\tan u)/(n-1)+(n-2)/(n-1)\int \sec^(n-2) u \, du`

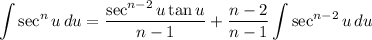
Hence:

`\displaystyle S = (1)/(2)\left((\sec \theta \tan\theta)/(2)\Big|_(0)^(\pi /3) + (1)/(2) \int_0^(\pi /3) \sec \theta\, d\theta\right)`

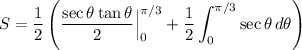
This is a common integral:

`\displaystyle S = (1)/(2)\left((\sec \theta \tan\theta)/(2)+ (1)/(2) \left(\ln \left(\sec \theta + \tan\theta\right)\right)\Bigg|_(0)^(\pi /3) \right)`

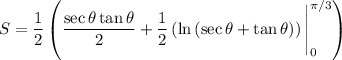
Evaluate. Hence:

`\displaystyle \begin{aligned} S = (1)/(2)\left[\left((\sec(\pi)/(3)\tan(\pi)/(3))/(2)+(1)/(2)\ln\left(\sec(\pi)/(3)+\tan(\pi)/(3)\right)\right) \\ - \left((\sec0\tan0)/(2)+(1)/(2)\ln\left(\sec 0 +\tan 0\right)\right)\right] \end{aligned}`

Evaluate:

`\displaystyle \begin{aligned} S &=(1)/(2) \left[ \left(((2)\left(√(3)\right))/(2) + (1)/(2)\ln \left(2 + √(3)\right) \right)-\left(((1)(0))/(2) + (1)/(2)\ln \left(1+0\right) \right) \right] \\ \\&= (1)/(2)\left(√(3) + (1)/(2) \ln \left(2+√(3)\right)\right) \\ \\ &\approx 1.1953 \end{aligned}`

Thus, the length of the arc is about 1.1953 units.