Answer:
Explanation:
Given g (x) =
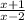 and
and
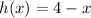 , we are to find
, we are to find
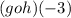
First we need to get
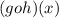
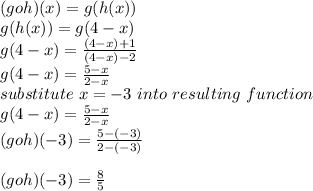
Hence

Also given f(x) = x and g(x) = 1/x, we are to find
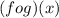
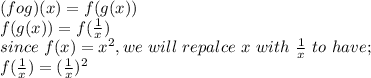
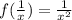
For the pair of function f(x) = 2/x and g(x) = 2/x
f(g(x)) = f(2/x)
f(2/x) = 2/(2/x)
f(2/x) = 2*x/2
f(2/x) = x
Hence f(g(x)) = x
For the pair of function f(x) = x-2/3 and g(x) = 2-3x
f(g(x)) = f(2-3x)
f(2-3x) = (2-3x-2)/3
f(2-3x) = -3x/3
f(2-3x) = -x
f(g(x)) = -x for the pair of function
For the pair of function f(x) = x/2 - 2 and g(x) = x/2 + 2
f(g(x)) = f(x/2 + 2)
f(x/2 + 2) = f((x+4)/2)
f((x+4)/2) = [(x+4)/2]/2 - 2
f((x+4)/2) = (x+4)/4 - 2
find the LCM
f((x+4)/2) = [(x+4)-8]/4
f((x+4)/2) = (x-4)/4
Hence f(g(x)) for the pair of function is (x-4)/4