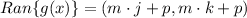Answer:
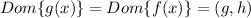 .
.
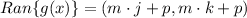
Explanation:
From Mathematics we remember that the domain of a functions corresponds to the set of values of the independent variable (
 in this case) so that images exist and the range of a function is the set of images.
in this case) so that images exist and the range of a function is the set of images.
In this case, we know the domain and range of
 and we must find the domain and range of
and we must find the domain and range of
 .
.
Domain
The domain of
 is the domain of
is the domain of
 . That is,
. That is,
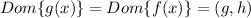 .
.
Range
We have to define the bounds of the range of
 , given that range
, given that range
 is modified by streching and horizontal translation operations:
is modified by streching and horizontal translation operations:
Lower bound (
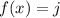 )
)
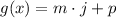
Upper bound (
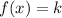 )
)
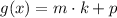
In consequence, the range of
 is
is