Answer:
Explanation:
Let
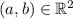 , a reflection over the x-axis consists in the following operation:
, a reflection over the x-axis consists in the following operation:
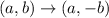
If we know that
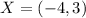 and
and
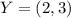 , then the points translated over the x-axis are
, then the points translated over the x-axis are
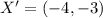 and
and
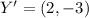 , respectively. The most precise description of the shape is a rectangle for the following facts:
, respectively. The most precise description of the shape is a rectangle for the following facts:
1)
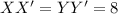 and
and
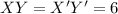 .
.
2)
 and
and
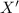 have the same x-component.
have the same x-component.
3)
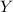 and
and
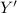 have the same x-component.
have the same x-component.
4)
 and
and
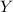 have the same y-component.
have the same y-component.
5)
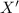 and
and
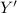 have the same y-component.
have the same y-component.
A representation of the shape is included below as attachment.