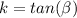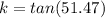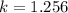Answer:
The length of the third side is
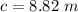
The tangent of the angle for which 6.9 m is the opposite side is
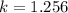
Step-by-step explanation:
From the question we are told that
The first side is a = 6.9 m
The second side is b = 5.5 m
Generally apply Pythagoras theorem
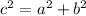
=>
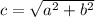
=>

=>
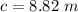
From sin rule we have that
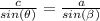
Generally from a right triangle the angle
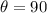
So
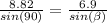
=>
![\beta = sin ^(-1)[(6.9)/(8.82) ]](https://img.qammunity.org/2021/formulas/physics/high-school/lwqw7iwfw2yk0mar2ukdl3bjy9cr0uqe14.png)
=>
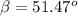
Generally the tangent of the angle for which 6.9 m is the opposite side is mathematically represented as