Question

Use the Distance Formula and the Pythagorean Theorem to find the distance between each pair of points. M (10, −4) and N (2, −7)

Answer 1

Distance formula: d = √(x2-x1)²+(y2-y1)²

= √(2-10)²+(-7-(-4))²

= √-8²+(-3)²

= √64+9

= √73

≈ 8.54

Best of Luck!

Answer 2

`d=√(73)\approx8.54`

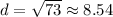
Explanation:

So we have the two points (10,-4) and (2,-7).

And we want to find the distance between them using the Distance Formula and the Pythagorean Theorem. Let's do each one individually.

1) Distance Formula.

The distance formula is:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

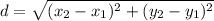
Let's let (10,-4) be (x₁, y₁) and let's let (2,-7) be (x₂, y₂). So:

`d=\sqrt{((2)-(10))+((-7)-(-4))^2`

Simplify:

`d=\sqrt{(2-10)^2+(-7+4)^2`

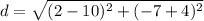
Subtract:

`d=\sqrt{(-8)^2+(-3)^2`

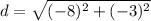
Square:

`d=√(64+9)`

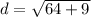
Add:

`d=√(73)`

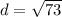
Approximate:

`d\approx8.54`

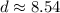
So, the distance between (10,-4) and (2,-7) is approximately 8.54 units.

2) Pythagorean Theorem

Please refer to the graph.

So, we want to find the distance. This will be the length of the red line, or the hypotenuse.

First, let's find the length of the two legs.

The longer leg will be the difference between the two x-coordinates. So, the length of the longer leg is:

`(10-2)=8`

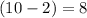
Note: It doesn't matter if we do 2-10, which gives -8, since we are going to square anyways. Also, distance is always positive, so 8 would be our answer.

And the shorter leg is the difference between the two y-coordinates. Namely:

`(-7-(-4))=-3=3`

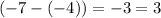
So, the shorter leg is 3 units.

So now, we can use the Pythagorean Theorem, which is:

`a^2+b^2=c^2`

Substitute 8 for a and 3 for b. So:

`(8)^2+(3)^2=c^2`

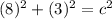
Square:

`64+9=c^2`

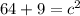
Add:

`c^2=73`

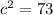
Take the square root:

`c=√(73)\approx8.54`

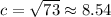
This is the same as our previous answer, so we can confirm that it's correct.

So, using both the distance formula and the Pythagorean Theorem, the distance between the two points is approximately 8.54.

And we're done!