Question

What is the first step when rewriting y = 6x2 + 18x + 14 in the form y = a(x – h)2 + k?

Answer 1

The first step when rewriting
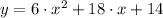`y = 6\cdot x^(2)+18\cdot x + 14` consists in applying distributive property. (Step 2).

Explanation:

We present the procedure, in which
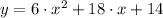`y = 6\cdot x^(2)+18\cdot x + 14` is transformed into the form
`y = a\cdot (x-h)^(2) + k`:

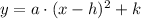1)
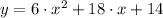`y = 6\cdot x^(2)+18\cdot x + 14` Given

2)
`y = 6\cdot \left( x^(2)+3\cdot x + (7)/(3)\right)` Distributive property/
`(a\cdot c)/(b\cdot c) = (a)/(b)`

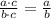
3)
`y = 6\cdot \left[x^(2)+3\cdot x + (7)/(3)+\left(-(1)/(12) \right)+(1)/(12) \right]` Modulative property/Existence of the additive inverse.

4)
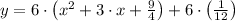`y = 6\cdot \left(x^(2)+3\cdot x+(9)/(4) \right)+6\cdot \left((1)/(12)\right)` Definition of subtraction/Associative and distributive properties.

5)
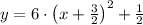`y = 6\cdot \left(x+(3)/(2) \right)^(2)+(1)/(2)` Perfect square trinomial/
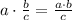`a \cdot (b)/(c) = (a\cdot b)/(c)`/Result.

As we can see, the first step when rewriting
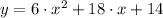`y = 6\cdot x^(2)+18\cdot x + 14` consists in applying distributive property. (Step 2).