Question

a person standing near the top of the Eiffel tower(approximately 300.6 meters) notices a car wreck some distance from the tower. If the angle of depression from the person's eyes to the wreck is 32°, approximately how far away is the accident from the base of the tower? ​

Answer 1

481.06

Explanation:

Let's visualise this case in a right angled triangle.

Height = 300.6 m

Angle of depression = Angle of elevation = 32°

So,

`\sin(32) = (300.6)/(hypotenuse)`

`= > 0.5299192642 = (300.6)/(hypotenuse)`

`= > hypotenuse = \frac{300.6} {0.5299192642 }`

`= 567.2562224244 m`

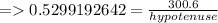
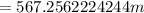
Hypotenuse = Line of sight = 567.25 m

Also,

`\cos(32) = (base)/(567.2562224244)`

`= > 0.8480480962 = (base)/(567.2562224244)`

`= > base = 0.8480480962 * 567.2562224244 = 481.0605594599`

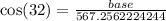
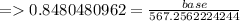
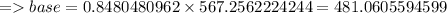
Hence Base = Distance between the spot of accident & the base of the tower = 481.06 m