Question

Simplify the following expression.

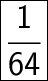
Answer 1

`\huge{ \boxed{ \sf{ (1)/(64) }}}`

Explanation:

`\star{ \sf{ \: \: \: {4}^{ - (11)/(3) } / {4}^{ - (2)/(3) } }}`

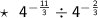
`\underline{ \: \text{Remember!}} :` If
`\sf{ {x}^(a) \: and \: {x}^(b) }` are two algebraic terms , then their quotient is given by
`\sf{ {x}^(a) / {x}^(b) = {x}^(a - b) }`

i.e To divide two terms with the same base, the power of divide is subtracted from the power of the dividend and the same base is taken.

`\mapsto{ \sf{ {4}^{ - (11)/(3) - ( - (2)/( 3)) } }}`

`\sf{We \: know \: that : ( - ) * ( - ) = ( + )}`

`\mapsto{ \sf{ {4}^{ - (11)/(3) + (2)/(3) } }}`

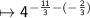
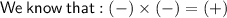
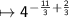
Now, Simplify : -11/3 and 2/3

While performing the addition or subtraction of like fraction, you just have to add or subtract the numerator respectively in which the denominator is retained same.

`\mapsto{ \sf{ {4}^{ ( - 11 + 2)/(3) } }}`

`\underline{ \text{Remember!}} :` The negative and positive integers are always subtracted but posses the sign of the bigger integer

`\mapsto{ \sf{ {4}^{ ( - 9)/(3) } }}`

Divide -9 by 3

`\mapsto{ \sf{ {4}^( - 3) }}`

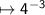
`\underline{ \text{Remember!}} :` If
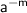`\sf{ {a}^( - m)}` is an algebraic term , where m is a negative integer , then

`\sf{ {a}^( - m) = \frac{1}{ {a}^(m) } }`

`\mapsto{ \sf{ \frac{1}{ {4}^(3) } }}`

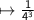
Evaluate the power : 4³

`\mapsto{ \sf{ (1)/(64) }}`

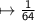
Hope I helped!

Best regards!:D

~
`\text{TheAnimeGirl}`