Question

The length of a reſtangle is 3 ft more than the width. The perimeter is is 62 ft. Find the length and

width of the rectangle.

Answer 1

Solution:-

Given that length of rectangle is 3 ft more than its breadth . Also , perimeter of rectangle is 62 ft . And we are asked to find the Length and breadth .

So , we know we can find perimeter of rectangle as :

`\boxed{\red{\bf \dag Permiter_(rectangle)=2(l+b)}}`

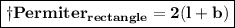
Now , let us take the

• Breadth be x .
• Length be x + 3 .

So , as per Question :

`\tt :\implies Perimeter=2(l+b)`

`\tt :\implies 62 \cancel{ft.} = 2( x + 3 + x ) \cancel{ft.}`

`\tt :\implies 62 = 2 ( 2x + 3 )`

`\tt :\implies 62 = 4x + 6`

`\tt :\implies 4x = 62 - 6`

`\tt :\implies4x = 56.`

`\tt :\implies x =\frac{\cancel{56}}{\cancel{4}}`

`\underline{\boxed{\red{\tt\longmapsto \:\:x\:\:=\:\:14}}}`

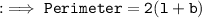
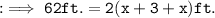
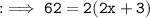
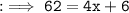
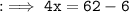
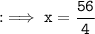
Hence we got x as 14 .

So , let's put the value in our assumption:

• 
  `\boxed{\green{\bf \pink{\dag} Length = x + 3 = 14 + 3 = 17 ft.}}`

• 
  `\boxed{\green{\bf \pink{\dag} Breadth = x = 14 ft.}}`