Question

Find the equation for the circle with center (4,5) and passing through (-3,5).

Answer 1

`(x-4)^2+(y-5)^2=49`

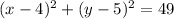
Explanation:

So we want to find the equation of a circle with the center at (4,5) and which passes through the point (-3,5).

First, recall the standard form for a circle, given by the equation:

`(x-h)^2+(y-k)^2=r^2`

Where (h,k) is the center and r is the radius.

We already know that the center is (4,5). So, substitute 4 for h and 5 for k. Therefore, our equation is now:

`(x-4)^2+(y-5)^2=r^2`

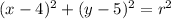
Now, we need to find the radius.

Remember that our circle passes through the point (-3,5). In other words, when x is -3, y is 5. So, substitute -3 for x and 5 for y to solve for r. Therefore:

`(-3-4)^2+(5-5)^2=r^2`

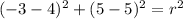
Subtract within the parentheses:

`(-7)^2+(0)^2=r^2`

Square:

`49=r^2`

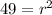
Square root:

`r=7`

Therefore, the radius is 7.

So, substitute 7 into our equation, we will acquire:

`(x-4)^2+(y-5)^2=(7)^2`

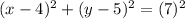
Square:

`(x-4)^2+(y-5)^2=49`

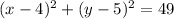
So, our equation is:

`(x-4)^2+(y-5)^2=49`

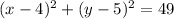
And we're done!