Answer:
The answer is
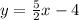
Explanation:
Equation of a line is y = mx + c
where
m is the slope
c is the y intercept
To find the equation of the perpendicular line we must first find the slope of the original line
The original line is y = - 2/5x + 3
Comparing with the general equation above
Slope/m = - 2/5
Since the lines are perpendicular to each other the slope of the perpendicular line is the negative inverse of the original line
So we have
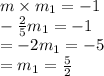
So the slope of the perpendicular line is
5/2
So the equation of the line using point
(2, 1) and slope 5/2 is
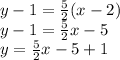
We have the final answer as
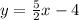
Hope this helps you