Question

What are the solutions of 3t + 2 < 7 or -4t + 5 < 1? Graph the solutions and put each solution in interval notation.

Answer 1

`\displaystyle (-∞, 2(1)/(3)) ∪ (1, ∞) \\ \\ 2(1)/(3) > t \:OR\: 1 < t`

Explanation:

3t + 2 < 7 OR −4t + 5 < 1

- 2 - 2 - 5 - 5

___________________

`\displaystyle (3t)/(3) < (7)/(3) \:OR\: (-4t)/(-4) < (-4)/(-4) \\ \\ t < 2(1)/(3) \:OR\: t >1`

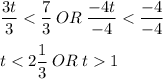
**Whenever you divide\multiply by a negative integer, you reverse the inequality symbol given to you initially.

Extended Information on Inequalities

≤, ≥ [dark circle with a dark line (brackets when writing in Interval Notation)]

<, > [light circle with a dashed line (parentheses when writing in Interval Notation)]

I am delighted to assist you at any time.

As you can see in the above graph, the graph is connected ALTOGETHER. Be aware that this will not ALWAYS be the case because a majourity of these graphs are seperated, pointing in OPPOSITE directions.