Answer:
Solution : 3
Explanation:
Well there are actually two approaches to this. (1) You could apply the power rule, making it a bit simpler, or (2) use the approach given. Let's just use the approach given so you can learn it as assigned that way:
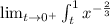
Funny thing is we will use the power rule anyhow when solving this problem. We want to start by evaluating x^-2/3 on the interval [t to 1].
![\mathrm{Apply\:the\:Power\:Rule}:\quad \int x^adx=(x^(a+1))/(a+1)\\=> \left[\frac{x^{-(2)/(3)+1}}{-(2)/(3)+1}\right]^1_t\\\\=> \left[3x^{(1)/(3)}\right]^1_t\\\\\mathrm{Compute\:the\:boundaries}\\=> 3-3t^{(1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/college/wtwv3s5sfa3aadcm6onygdpi8482bn4dg3.png)
And now you know that we would have to substitute this value, 3 - 3t^1/3, back into the primary expression.
