Answer:
See below.
Explanation:
So we have the rational function:
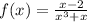
Now, remember that the domain of rational functions will always be all real numbers... except when the domain is 0.
In other words, to find our domain restrictions, we simply need to solve for the zeros of our denominator.
So, set the denominator to 0 and solve for x:
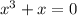
Factor out an x:
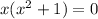
Zero Product Property:
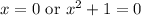
So, our x cannot be 0 according to our first answer.
For the second answer, subtract 1 from both sides:
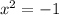
This isn't possible on our coordinate plane. We have no real solution.
Therefore, our only domain restriction is that x cannot be equal to 0.
Therefore, our domain is all real numbers except for x=0.
In set notation, this is:
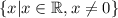
And in interval notation, this is:
