Answer:
a)
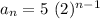
b)

c)
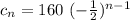
Explanation:
a) Geometric sequence with first term 5 and common ratio 2, where the nth term can be calculated via:
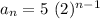
The first five terms are:
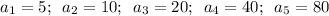
b) Geometric sequence with first term 100 and common ratio 1/2, where the nth term can be calculated via:

The first five terms are:
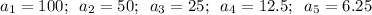
c) Geometric sequence with first term 160 and common ratio -1/2, where the nth term can be calculated via:
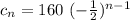
The first five terms are:
