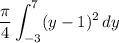Question

The following curves bound an area: y = 2x + 1, y = -3, and x = 3. Set up the integral to find the VOLUME if this area is revolved about the line x = 3. DO NOT EVALUATE.

Answer 1

First note the intersections of each pair of lines.

x = 3 ⇒ y = 2•3 + 1 = 7 ⇒ (3, 7)

y = -3 ⇒ -3 = 2x + 1 ⇒ x = -2 ⇒ (-2, -3)

y = -3 and x = 3 ⇒ (3, -3)

Using the disk method, we consider disks with thickness ∆y and radius equal to the horizontal distance between the line y = 2x + 1 (or x = (y - 1)/2) and the axis of revolution, x = 3. Each disk will then contribute a volume of

∆V = π (radius)² (thickness) = π/4 (y - 1)² ∆y

As we let ∆y go to zero and let the number of disks go to infinity, the total volume of the resulting cone will be given by the integral

`\displaystyle \frac\pi4 \int_(-3)^7 (y-1)^2 \, dy`