Answer:
B: 2029
Explanation:
Interest Formula
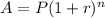
A= amount
P= initial amount
r= rate/percentage
n= years
All we have to do is plug in the numbers from the word problem to get:
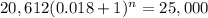
From here we solve for n:

Get the natural log (ln) of both sides:
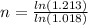
n is approximately 10.823
n is the number of years it will take for the population to reach 25,000 people.
2019+10
=2029