Question

If
`f(x)=x^2-2` and
`g(x)=3x`, what is
`(f\circ g)(2)`?

Answer 1

`\large\boxed{34}`

Explanation:

`f(x) = x^2 - 2`

`g(x) = 3x`

`(fog)(2)`

Find g(2)

`g(x) = g(2)`

`x=2`

`3x = 3(2) = 6`

`g(2) = 6`

Find f(6)

`f(x) = x^2-2`

Substitute

`f(6) = x^2 - 2`

`x^2 - 2 = 6^2 - 2`

`36 - 2 = 34`

`\large\boxed{34}`

Hope this helps :)

Answer 2

`\boxed{f(6) = 34}`

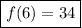
Explanation:

Composition of functions occurs when we have two functions normally written similar or exactly like f(x) & g(x) - you can have any coefficients to the (x), but the most commonly seen are f(x) and g(x). They are written as either f(g(x)) or (f o g)(x). Because our composition is written as
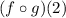`(f \circ g)(2)`, we are replacing the x values in the g(x) function with 2 and simplifying the expression.

`g(2) = 3(2)`

`g(2) = 6`

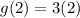
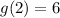
Now, because we are composing the functions, this value we have solved for now replaces the x-values in the f(x) function. So, f(x) becomes f(6), and we use the same manner as above to simplify.

`f(6) = (6)^2-2`

`f(6) = 36-2`

`f(6) = 34`

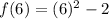
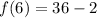
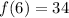
Therefore, when we compose the functions, our final answer is
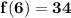`\bold{f(6) = 34}`.