Question

A ranger in a national park is driving at 36.2mi / h when a deer jumps into the road 205 ft ahead of the vehicle. After a reac tion time of t the ranger applies the brakes to produce and acceleration of - 8.83ft / (s ^ 2) What is the maximum reaction time al lowed if she is to avoid hitting the deer ? Answer in units of s. Need help ASAP please

Answer 1

Step-by-step explanation:

Given that,

Initial speed of a ranger, u = 36.2 mi/h

Distance dove by the ranger, d = 205 ft

Due to the application of brakes, the acceleration reached is 8.83 ft/s².

We need to find the maximum reaction time allowed if she is to avoid hitting the deer.

We know that,

1 mph = 1.46667 ft/s

36.2 mi/h = 53.09 ft/s

Let t is time.

Using second equation of kinematics to find it as follows :

`d=ut+(1)/(2)at^2\\\\ 205=53.09t-(1)/(2)* 8.83t^2\\\\4.415t^(2)-53.09t+205=0`

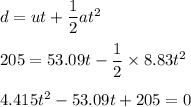
The above is a quadratic equation. We need to solve it for t as follows :

`t=x=(-\left(-53.09\right)-4\left(4.415\right)\left(205\right))/(2\cdot4.415),(-\left(-53.09\right)+4\left(4.415\right)\left(205\right))/(2\cdot4.415)\\\\t=-403.98\ s,416.01\ s`

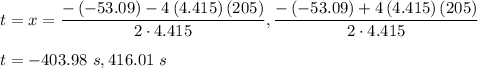
Hence, 416.01 seconds is the maximum reaction time allowed if she is to avoid hitting the deer.