Question

In a coordinate system in which the direction to the right is positive, what are the distance

and displacement of a person who walks 35meters to the left, 18meters to the right, and then
26meters to the left?

Answer 1

The distance is
`d = 79 \ m`

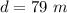
The displacement is 43 m to the left

Step-by-step explanation:

Generally the distance is mathematically represented as

`d = a + b + c`

substituting 35 meters for b, 18 meters for a and 26 meters for c

So

`d = 35 + 18 + 26`

`d = 79 \ m`

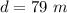
In the question we are going to assume the left direction is negative while right direction is positive

Generally the displacement is mathematically represented as

`D = x + y + z`

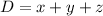
substituting (- 35) meters for y, (+ 18 )meters for x and (-26) meters for z

`D = 18 - 35 -26`

`D = - 43\ m`

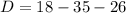
So the displacement is 43 meters to the left