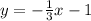Question

Write an equation for a line perpendicular to 3y−9x=−15 and passing through the point (9,-4)

Answer 1

y=-1/3x+5

Explanation:

A perpendicular line has to be the opposite reciprocal. And the the y intercept doesnt matter (y=mx+b) b doesnt matter

Answer 2

`y=-(1)/(3)x-1`

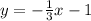
Explanation:

So we want to write an equation for a line perpendicular to 3y-9x=-15 and which passes through the points (9,-4).

First, let's determine the slope of our new line.

To do so, let's put the original equation into slope-intercept form. So we have:

`3y-9x=-15`

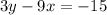
Add 9x to both sides:

`3y=9x-15`

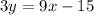
Divide both sides by 3:

`y=3x-5`

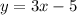
So, the slope of our original equation is 3.

Perpendicular lines have slopes who are negative reciprocals of each other.

In other words, to find the slope of our new line, we simply need to flip our old slope and add a negative.

Therefore, our new slope is -1/3.

Now, we can use the point-slope form to find the equation of our new line. The point-slope form is:

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point.

Let's substitute -1/3 for m and (9,-4) for (x₁, y₁), respectively. Therefore:

`y-(-4)=-(1)/(3)(x-9)`

Simplify:

`y+4=-(1)/(3)(x-9)`

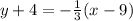
Distribute on the right:

`y+4=-(1)/(3)x+3`

Subtract 4 from both sides:

`y=-(1)/(3)x-1`

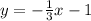
So, our new equation is:

`y=-(1)/(3)x-1`