Find the limit as h approaches 0

Question

asked Jul 2, 2021 190k views

1 Answer

Mohit Tanwani · Answer 1 · 2021-07-06T14:40:33+0000

Answer:

C.

Explanation:

We want to find the limit:

$\displaystyle \lim_(h\to 0) (√(2x+2h)-√(2x))/(h)$

Let's remove the square roots in the numerator by multiplying both layers by the conjugate. Hence:

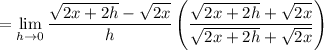
$\displaystyle =\lim_(h\to 0) (√(2x+2h)-√(2x))/(h)\left((√(2x+2h)+√(2x))/(√(2x+2h)+√(2x))\right)$

In the numerator, we have the difference of two squares pattern. The difference of two squares is:

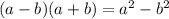
(a-b)(a+b)=a^2-b^2

So, our numerator is now:

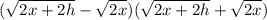
$(√(2x+2h)-√(2x))(√(2x+2h)+√(2x))\\$

Difference of two squares:

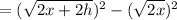
=(√(2x+2h))^2-(√(2x))^2

Simplify:

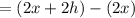
=(2x+2h)-(2x)

In the denominator, we can keep everything the same for now. Thus, our limit is simplified to:

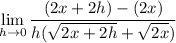
$\displaystyle \lim_(h\to 0) ((2x+2h)-(2x))/(h(√(2x+2h)+√(2x)))$

Subtract:

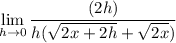
$\displaystyle \lim_(h\to 0) ((2h))/(h(√(2x+2h)+√(2x)))$

We can cancel the h:

$\displaystyle \lim_(h\to 0) (2)/(√(2x+2h)+√(2x))$

Now we can use direct substitution. So:

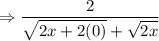
$\displaystyle \Rightarrow (2)/(√(2x+2(0))+√(2x))$

Simplify:

$\displaystyle =(2)/(√(2x)+√(2x))$

Combine like terms:

$\displaystyle =(2)/(2√(2x))$

Reduce:

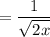
$\displaystyle =(1)/(√(2x))$

In conclusion:

$\displaystyle \lim_(h\to 0) (√(2x+2h)-√(2x))/(h)=(1)/(√(2x))$

Hence, our answer is C.