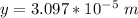Question

When reading the printout from a laser printer, you are actually looking at an array of tiny dots.

If the pupil of your eye is 4.2 mm in diameter when reading a page held 29 cm from your eye, what is the minimum separation of adjacent dots that can be resolved? (Assume light with a wavelength of 500 nm , and use 1.36 as the index of refraction for the interior of the eye.)
Express your answer using two significant figures.

Answer 1

The value is
`y = 3.097 * 10^(-5) \ m`

Step-by-step explanation:

From the question we are told that

The diameter of the pupil is
`d_p = 4.2 \ mm = 4.2 *10^(-3) \ m`

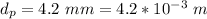
The distance of the page from the eye
`d = 29 \ cm = 0.29 \ m`

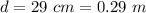
The wavelength is
`\lambda = 500 \ nm = 500 *10^(-9) \ m`

The refractive index is
`n_r = 1.36`

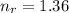
Generally the minimum separation of adjacent dots that can be resolved is mathematically represented as

`y = [ (1.22 * \lambda )/(d_p * n_r ) ]* d`

`y  = [ (1.22 *  500 *10^(-9) )/(4.2 *10^(-3) * 1.36) ]* 0.29`

`y  = 3.097 * 10^(-5) \  m`