Question

1. A ball rolls with a constant acceleration of 2.5 m/s^2 for 5.0 s with an initial velocity of 5.0 m/s. Calculate the ball’s distance from the starting point at 1.0 s intervals. Make a position-time graph for the object’s motion. In your response, show what you are given, the equation that you used, any algebra/work required, a table of data, and your graph.

Answer 1

Step-by-step explanation:

Given that the initial velocity of the ball is
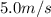`5.0 m/s`, the constant acceleration is
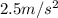`2.5 m/s^2`, and the time of motion is
`5.0 s`.

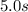Denote the initial velocity be u, constant acceleration by a, and the time by
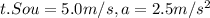`t. So u= 5.0 m/s, a= 2.5 m/s^2` and
`t= 5.0 s`.

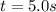From the equation of motion, the distance, s, covered by the object in time, t, starting with velocity u, having constant acceleration, a, is

`s=ut+\frac 12 at^2`

`\Rightarrow s= 5t+\frac 5 2 t^2\;\cdots(i)`

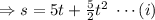
As the time interval is
`1.0 s`

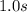
So the time after the 1st interval is 1 s and from equation (i) the distance covered from the starting point is,

`s_(t=1)=5* 1 +\frac 5 2 *1^2=7.5 m`.

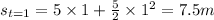The time after the 2nd interval is 2 s and from equation (i) the distance covered from the starting point is,

`s_(t=2)=5* 2 +\frac 5 2 *2^2=20 m`.

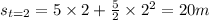Similarly, after the 3rd interval, t=3s

`s_(t=3)=5* 3 +\frac 5 2 *3^2=37.5 m`.

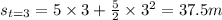After the 4th interval, t=4s

`s_(t=3)=5* 4 +\frac 5 2 *4^2=60 m`.

And finally, after the 5th interval, t=5s

`s_(t=3)=5* 5 +\frac 5 2 *5^2=87.5 m`.

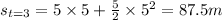The tabulated data and the position-time graph has been shown in the figure.