Question

Select the correct answer.

Consider this quadratic equation.
X^2+ 1 = 2x-3
Which expression correctly sets up the quadratic formula?

OA. -(-2) + 2)2 - 4(1)(4)
2(1)
OB.-(-2) + VE-2)2 – (1)(4)
2(2)
OC -2 + (-2)2 - 4(1)(4)
2(1)
OD. -2 + (2)2 – 4(1)(-2)
2(1)

Answer 1

A.
`\displaystyle{\frac{-(-2) \pm \sqrt{(2)^(2)-4(1)(4)}}{2(1)} }`

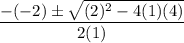
Find the values a, b, and c to substitute into the quadratic formula.

Remember:

Standard form

Notice how there are a, b, and c. Everything is left of the equal sign, leaving 0 on the right.

ax² + bx + c = 0

Quadratic formula

Notice how there are a, b, and c too, just like in standard form. After we find standard form, we can substitute a, b and c values into the quadratic formula.

`\displaystyle{x=\frac{-b \pm \sqrt{b^(2)-4ac}}{2a} }`

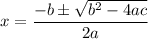
Step-by-step solution

Here are the steps we will follow:

1. Rearrange the equation from the question into standard form.
2. Determine the values for a, b, and c.
3. Substitute a, b, and c into the quadratic formula.
4. Compare options and simplify as needed.

Rearrange into standard form

Move everything to the left while keeping both sides equal.

x² + 1 = 2x – 3 Equation from the question

x² + 1 + 3 = 2x – 3 + 3 Add three to both sides.

x² + 1 + 3 = 2x -3 + 3 cancels out to 0.

x² + 4 = 2x Simplify.

x² + 4 – 2x = 2x – 2x Subtract 2x from both sides.

x² + 4 – 2x = 0 No numbers on the right side is the same as 0.

x² – 2x + 4 = 0 Rearrange to follow ax² + bx + c = 0.

Determine a, b, and c values

Find a, b, and c from standard form.

ax² + bx + c = 0 Standard form

x² – 2x + 4 = 0 No number attached to x² means a = 1.

a = 1, b = –2, and c = 4

Substitute into the quadratic formula

Substitute a = 1, b = –2, and c = 4 into the quadratic formula.

`\displaystyle{x=\frac{-b \pm \sqrt{b^(2)-4ac}}{2a} }`

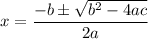
Here is how our formula set up should look:

`\displaystyle{x=\frac{-(-2) \pm \sqrt{(-2)^(2)-4(1)(4)}}{2(1)} }`

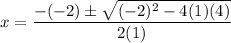
Compare answer options

Let's compare formula set up to the options in the question.

The denominator is 2(1). So, the answer is not option B.

Inside the square root, it says –4(1)(4). So, the answer is not option D.

This leaves us with either option A or option C.

Simplify

Before the ±, it says –(–2). When simplified, –(–2) is 2.

Option C has –2. So, the answer is not option C.

Inside the square root, it says (–2)², which is equal to 2².

When solving exponents of negative numbers,

• an odd exponent results in a negative product, and;
• an even exponent results in a positive product.

The exponent 2 is even.

(–2)² = 4

∵ (–2)² = 4 and 2² = 4

∴ (–2)² = 2²

(–2)² is the same as 2².

Therefore, the answer is option A.