Answer:
43 + 7i
Explanation:
Given: (1 + 5i)(3 - 8i)
To find: Multiplication and simplification
Solution:
i=
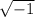 ,
,
Now, we simply open the brackets as follows:
(1 + 5i)(3 - 8i)
1(3 - 8i) + 5i (3 - 8i)
3 - 8i + 15i - 40
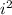
3 + 7i - 40
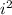 - (i)
- (i)
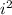 = i * i
= i * i
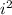 =
=
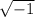 *
*
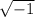
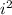 = -1
= -1
Now, put
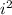 = -1 into the equation (i)
= -1 into the equation (i)
we get
⇒ 3 + 7i -40(-1)
⇒ 3 + 7i + 40
⇒ 43 + 7i
∴ Final Answer : 43 + 7i