Question

Sherry claims that the expression 1/x will always be equivalent to a repeating decimal whenever x is an odd number greater than 1

Answer 1

The correct options are :

b. 5

e. 25

Explanation:

The question is incomplete. The missing part is :

'' Which of these values will prove Sherry's claim is false :

a. 3

b. 5

c. 7

d. 11

e. 25 ''

One way to prove that Sherry's claim is false is finding one odd number greater than 1 that when we replace it in the denominator of the expression
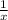`(1)/(x)` the result isn't equivalent to a repeating decimal.

Let's analyze each option :

• a. 3

3 is an odd number greater than 1 ⇒ If we replace in the expression
`(1)/(x)` ⇒

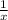`(1)/(3)` ≅ 0.3333 (repeating decimal)

The option a. 3 won't prove that Sherry's claim is false.

• b. 5

5 is an odd number greater than 1 ⇒ If we replace in the expression
`(1)/(x)` ⇒

`(1)/(5)=0.2`

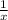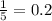
The result isn't a repeating decimal.

The option b. 5 will prove that Sherry's claim is false.

• c. 7

7 is an odd number greater than 1 ⇒ If we replace in the expression
`(1)/(x)` ⇒

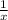`(1)/(7)` ≅ 0.1428 (repeating decimal)

The option c. 7 won't prove that Sherry's claim is false.

• d. 11

11 is an odd number greater than 1 ⇒ If we replace in the expression
`(1)/(x)` ⇒

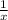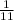`(1)/(11)` ≅ 0.0909 (repeating decimal)

The option d. 11 won't prove that Sherry's claim is false.

• e. 25

25 is an odd number greater than 1 ⇒ If we replace in the expression
`(1)/(x)` ⇒

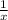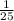`(1)/(25)` ≅ 0.04

The result isn't a repeating decimal

The option e. 25 will prove that Sherry's claim is false.