Question

A helicopter is ascending vertically with a speed of 5.32 m/s . At a height of 120 m above the Earth, a package is dropped from the helicopter.

How much time does it take for the package to reach the ground? [Hint: What is v0 for the package?]

Answer 1

Approximately
`5.52\; \rm s` (assuming that
`g = -9.81\; \rm m\cdot s^(-2)`.)

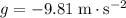Step-by-step explanation:

From the perspective of an observer on the ground, the package was initially moving with the helicopter. The initial velocity of that package (
`v_0`) would be the same as the velocity of the helicopter. In other words,
`v_0 = 5.32\; \rm m \cdot s^(-1)`.

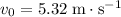Other quantities:

• 
  `a = g \approx -9.81\; \rm m \cdot s^(-2)`. (The
  `g` here is negative because the acceleration due to gravity points downwards.)
• 
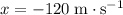  `x = -120\; \rm m \cdot s^(-1)` (The position of the package would have changed by
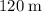  `120\; \rm m` by the time it reached the ground. The negative sign is because this position change also points downwards.)

There are two ways to find the time
`t` required for the package to reach the ground after it was dropped.

The first approach makes use of the SUVAT equation:

`\displaystyle x = (1)/(2)\, a\, t^2 - v_0\, t`.

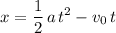For this question,
`x`,
`a`, and
`v_0` are already known. However, this approach would require solving a quadratic equation where the coefficient for the first-order term is non-zero.

An alternative approach is to solve for
`v_1`, the velocity of the package right before it reaches the ground. From the SUVAT equation that does involve time:

`\displaystyle {v_1}^(2) - {v_0}^(2) = 2\, a\, x`.

Again,
`x`,
`a`, and
`v_0` are already known. Solve for
`v_1`:

`\begin{aligned}v_1 &= \sqrt{2\, a\, x + {v_0}^2} \\ &\approx √(2* (-9.81) * (-120) + 5.32^2) \approx -48.81293\; \rm m \cdot s^(-1)\end{aligned}`.

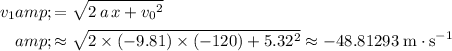Calculate time from the change in velocity:

`\displaystyle t = (v_1 - v_0)/(a) \approx 5.52\; \rm s`.