Question

15. If x=a Sin2t (I+Cos2t) and y=b Cos 2t (1-Cos2t) then find
dy/dx at =22/7*4
​

Answer 1

By the chain rule,

`(\mathrm dy)/(\mathrm dx)=(\mathrm dy)/(\mathrm dt)(\mathrm dt)/(\mathrm dx)\implies(\mathrm dy)/(\mathrm dx)=((\mathrm dy)/(\mathrm dt))/((\mathrm dx)/(\mathrm dt))`

It looks like we're given

`\begin{cases}x=a\sin(2t)(1+\cos(2t))\\y=b\cos(2t)(1-\cos(2t))\end{cases}`

where a and b are presumably constant.

Recall that

`\cos^2t=\frac{1+\cos(2t)}2`

`\sin^2t=\frac{1-\cos(2t)}2`

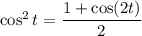
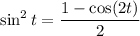
so that

`\begin{cases}x=2a\sin(2t)\cos^2t\\y=2b\cos(2t)\sin^2t\end{cases}`

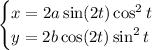
Then we have

`(\mathrm dx)/(\mathrm dt)=4a\cos(2t)\cos^2t-4a\sin(2t)\cos t\sin t`

`(\mathrm dy)/(\mathrm dt)=-4b\sin(2t)\sin^2t+4b\cos(2t)\sin t\cos t`

`\implies(\mathrm dy)/(\mathrm dx)=(4b\cos(2t)\sin t\cos t-4b\sin(2t)\sin^2)/(4a\cos(2t)\cos^2t-4a\sin(2t)\cos t\sin t)`

`\implies\boxed{(\mathrm dy)/(\mathrm dx)=\frac ba\tan t}`

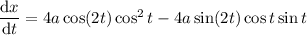
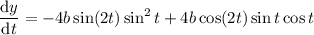
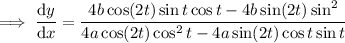
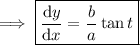
where the last reduction follows from dividing through everything by
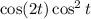`\cos(2t)\cos^2t` and simplifying.

I'm not sure at which point you're supposed to evaluate the derivative (22/7*4, as in 88/7? or something else?), so I'll leave that to you.