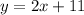Answer:
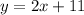
Explanation:
So we know that the slope is 2 and the lines passes through the point (-5,1).
We can use the point-slope form. The point-slope form is:
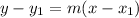
Where m is the slope and (x₁, y₁) is a point.
So, let's substitute 2 for m and (-5,1) for (x₁, y₁), respectively. Therefore:
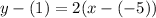
Simplify:
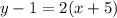
Distribute the 2:
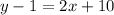
Add 1 to both sides:
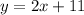
So, the equation of our line is: