Answer:
The circle is centered at (4,-6) and has a radius of √12.
Explanation:
The standard form for the circle equation is:

You have:
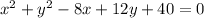
First complete the square for the 'x' terms:
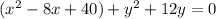
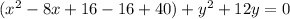
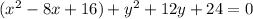
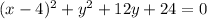
The 'x' terms are now in standard form. Work on the 'y' terms by completing the square once again:
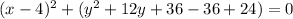
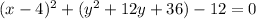
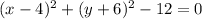
Add the 12 to the other side:
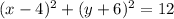
The circle is centered at x = 4, y = -6, and has a radius of √12.