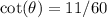Question

Find the exact values of the remaining five trigonometric functions of theta, suppose theta is an angle in the standard position whose terminal side is in Quadrant I and tan(theta)= 60/11

Answer 1

`\sin(\theta)=60/61\text{ and } \csc(\theta)=61/60\\\cos(\theta)=11/61\text{ and } \sec(\theta)=61/11\\\tan(\theta)=60/11\text{ and } \cot(\theta)=11/60`

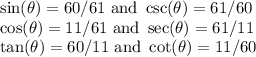
Explanation:

So, we know that:

`\tan(\theta)=60/11\text{ and } 90\textdegree<\theta<0`

Since θ is in QI, this means that all of our trig ratios will be positive. Recall All Students Take Calculus. Since it's QI, we refer to A in All. The A tells us that all the ratios will be positive.

Now, let's figure out the remaining ratios knowing that all of them is positive. First, let's find the hypotenuse. Recall that tangent is the ratio of the opposite side to the adjacent side. So, we can use the Pythagorean Theorem to find the hypotenuse. So:

`a^2+b^2=c^2`

Substitute 60 for a and 11 for b:

`60^2+11^2=c^2`

Solve for c. Square both numbers:

`3600+121=c^2`

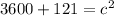
Add:

`c^2=3721`

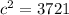
Take the square root of both sides:

`c=61`

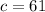
Therefore, the hypotenuse is 61.

So, our side lengths are: Opposite=60; Adjacent=11; and Hypotenuse=61.

Now that we know the lengths, we can find the other trig ratios:

Sine and Cosecant:

`\sin(\theta)=opp/hyp`

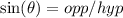
Substitute 60 for Opp and 61 for Hyp:

`\sin(\theta)=60/61`

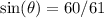
Cosecant is the reciprocal of sine. So:

`\csc(\theta)=61/60`

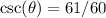
Cosine and Secant:

`\cos(\theta)=adj/hyp`

Substitute 11 for Adj and 61 for Hyp:

`\cos(\theta)=11/61`

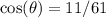
Secant is the reciprocal of cosine. So:

`\sec(\theta)=61/11`

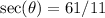
Tangent and Cotangent:

We are already given that tangent is:

`\tan(\theta)=60/11`

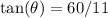
Cotangent is the reciprocal of tangent. So:

`\cot(\theta)=11/60`