Question

(100) What’s the distance of all the sides combined, add the method.

Answer 1

10cm2

Explanation:

Answer 2

As AE and BD intersect:

• ∠ACB and ∠ECD are vertically opposite angles and are therefore congruent.

As AB is parallel to ED:

• ∠BAC and ∠DEC are alternate interior angle and are therefore congruent.

• ∠ABC and ∠EDC are alternate interior angle and are therefore congruent.

Therefore, we can use SSS Similarity Theorem to find the lengths of the sides:

`\sf (AC)/(EC)=(BC)/(DC)=(AB)/(ED)`

`\implies \sf (400)/(1000)=(300)/(ED)`

`\implies \sf 400 \cdot ED=300 \cdot 1000`

`\implies \sf ED=(300000)/(400)=750`

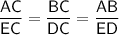
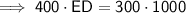
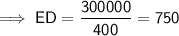
**The length of BC and CD cannot be determined without knowing an angle**

Therefore, the remainder of the calculations are based on the assumption that ∠BAC and ∠DEC are 90°

If ∠BAC = 90° then BC can be calculated using Pythagoras' Theorem

⇒ AB² + AC² = BC²

⇒ 300² + 400² = BC²

⇒ BC² = 250000

⇒ BC = 500

Using the side ratios stated previously:

`\sf (AC)/(EC)=(BC)/(DC)=(AB)/(ED)`

`\implies \sf (400)/(1000)=(500)/(DC)`

`\implies \sf 400 \cdot DC=500 \cdot 1000`

`\implies \sf DC=(500000)/(400)=1250`

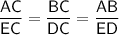
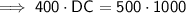
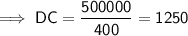
Therefore, the distance of each side is:

• AC = 400 m
• AB = 300 m
• BC = 500 m
• EC = 1000 m
• ED = 750 m
• DC = 1250 m

Assuming the sides are the solid lines marked with arrows only:

⇒ Total distance = AB + BC + DC + ED

= 300 + 500 + 1250 + 750

= 2800 m