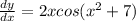Answer:
Explanation:
Given:
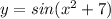
Find:
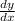
For this problem, it looks like we are going to use the chain rule. We have to functions, let's label them:
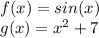
Let's remember that the chain rule is:
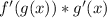 or
or
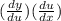
Since these functions are basic, I will be using the
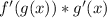 rule, but both rules always work. We need to find
rule, but both rules always work. We need to find
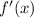 and
and
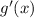
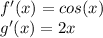
Remember that the derivative of
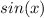 is
is
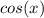 . Make sure you know all your trig derivatives. Now that we know all our variables, we can plug them in. We will take
. Make sure you know all your trig derivatives. Now that we know all our variables, we can plug them in. We will take
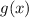 and plug it into
and plug it into
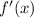 and multiply it all by
and multiply it all by
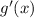 .
.
![[cos(x^2+7)][2x]=2xcos(x^2+7)](https://img.qammunity.org/2021/formulas/mathematics/high-school/mc4gv0enf9t2gj1vat7bb9tuwcnu1w2f7d.png)
Since nothing else can be done to reduce this expression, your answer is: