Answer:
![(dy)/(dx)[\sqrt[3]{1+8x} ] = \frac{8}{3\sqrt[3]{(1+8x)^2} }](https://img.qammunity.org/2021/formulas/advanced-placement-ap/high-school/wxvs58sz4j7qtzqzs3c8wxpjl4gzsffjr5.png)
Step-by-step explanation:
We need to use the chain rule, and you correctly identified it; however, you did not apply it correctly. Let's review it.
The chain rule is
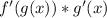
To solve, we need
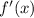 and
and
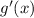 . Let's find them.
. Let's find them.
![f'(x)= (d)/(du) [\sqrt[3]{u} ] = (d)/(du) [u^(1)/(3) ] = (1)/(3)u^(-2)/(3) = (u^(-2)/(3) )/(3) = (1)/(3u^(2)/(3) ) \\g'(x)= (d)/(dx) [1+8x] = 8](https://img.qammunity.org/2021/formulas/advanced-placement-ap/high-school/gi7gmukpnylbau1u9cdz1ebon3vnmzosp7.png)
For both these derivatives, I used the power rule. For
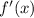 , I just simplified it completely to make it look nicer. Now that we know everything, we need to plug it into the chain rule:
, I just simplified it completely to make it look nicer. Now that we know everything, we need to plug it into the chain rule:
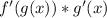
Take the
 function and put it into
function and put it into
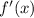 and multiply all that by
and multiply all that by
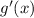 .
.
![((1)/(3(1+8x)^(2)/(3) ) )((8)/(1) ) = (8)/(3(1+8x)^(2)/(3) ) = \frac{8}{3\sqrt[3]{(1+8x)^2} }](https://img.qammunity.org/2021/formulas/advanced-placement-ap/high-school/8f4pzv689easki21a6ximgurun8spq0wlz.png)
So, your derivative is
![\frac{8}{3\sqrt[3]{(1+8x)^2} }](https://img.qammunity.org/2021/formulas/advanced-placement-ap/high-school/yv4x8wi3j4fbpeghgh6rbmvaqrp2kf3xfw.png)