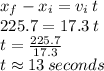Question

A ranger in a national park is driving at 11.8mi / h when a deer jumps into the road 242 ft ahead of the vehicle. After a reaction time of t the ranger applies the brakes to produce and acceleration of -9.18ft/s^2 What is the maximum reaction time allowed if she is to avoid hitting the deer? Answer in units of s.

Answer 1

The maximum reaction time is approximately 13 seconds

Step-by-step explanation:

In order to answer this problem let's start by converting the speed of the ranger's vehicle from miles per hour into feet per second, knowing that 1 mile is the same as 5280 ft and i hour is 3600 seconds:

`11.8\, (mi)/(h) =11.8 \,(5280\,ft)/(3600\,s) \approx 17.3\,(ft)/(s)`

Now, with this information, we set the equation for the amount of time needed to reduce the speed from 17.3 ft/s to full stop (0 ft/s):

`v_f-v_i=-9.18 \,t\\0-17.3=-9.18\,t\\t=(17.3)/(9.18) \,s\\t\approx 1.88\,s`

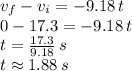
Now, the space covered during these 1.88 s when the vehicle reaches full stop while it decelerates is calculated via:

`x_f-x_i=v_i\,t + (1)/(2) a\,t^2\\x_f-x_i=17.3\,t-(9.18)/(2) \,t^2\\x_f-x_i=17.3\,(1.88)-4.59\,(1.88)^2\\x_f-x_i=16.3\,ft`

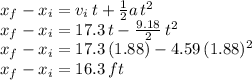
So, the maximum amount of time the ranger has to react and press the break while driving at 17.3 ft/s is the time to cover 242 ft minus 16.3 ft = 225.7 ft

During 225.7 ft the ranger could be driving in uniform motion (with speed 17.3 ft per second), we find the time to cover such:

`x_f-x_i=v_i\,t\\225.7 = 17.3\,t\\t= (225.7)/(17.3) \\t\approx 13\, seconds`