Question

The graph shows triangle A B C is congruent to triangle D E F ​by S A S, where segment C A is congruent to segment F D, segment C B is congruent to segment F E, and angle C is congruent to angle F

Move the statements to the table to create a series of transformations that will map triangle A B C onto triangle D E F to show that the two triangles are congruent.
What is Transformation 1 and. Transformation 2

Answer 1

reflection on x-axis

then translations right 3 units & down 2 units

Answer 2

To map triangle ABC onto triangle DEF by SAS congruence, Transformation 1 involves a translation where points A, B, and C move to D, E, and F respectively. Transformation 2 is a 180-degree rotation around point F.

To create a series of transformations mapping triangle ABC onto triangle DEF:

1. Transformation 1 - Translation:

- Translation is the first transformation. It involves moving the entire triangle in a specific direction.

-
`\(A(-2, 4) \rightarrow D(1, -2)\)`

-
`\(B(-1, 3) \rightarrow E(2, -1)\)`

-
`\(C(-3, 2) \rightarrow F(0, 0)\)`

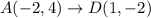
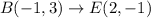
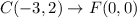
2. Transformation 2 - Rotation:

- After translation, a rotation is performed around a specific point.

- In this case, it's a 180-degree rotation, as angle C is congruent to angle F.

-
`\(D(1, -2) \rightarrow D'(1, 2)\)`

-
`\(E(2, -1) \rightarrow E'(-2, 1)\)`

-
`\(F(0, 0) \rightarrow F'(0, 0)\)`

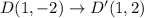
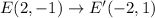
So, Transformation 1 is a translation, and Transformation 2 is a rotation of 180 degrees.