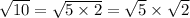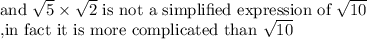Question

If the number under the square root radical has no perfect souare

factors, then it cannot be simplified further.
TRUE
FALSE

Answer 1

true

Explanation:

Examples :

180 = 5 × 2² × 3²

Then

The number 180 has perfect square factors which are 2 and 3

Then

The number √180 can be simplified because:

`√(180) =\sqrt{5* 2^(2)* 3^(2)}`

`=\sqrt{5* \left( 2* 3\right)^(2) }`

`=\sqrt{5* \left( 6\right)^(2) }`

`=√(5) * \sqrt{6^(2)}`

`=6√(5)`

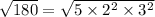
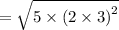
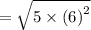
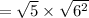
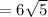
On the other hand :

10 = 5 × 2

Then

The number 10 has no perfect square factors

Then

The number √10 cannot be simplified because:

`√(10) =√(5* 2) =√(5) * √(2)`

`\text{and} \ √(5) * √(2) \ \text{is not a simplified expression of} \ √(10) \ \\\text{,in fact it is more complicated than} \ √(10)`