Question

Please help me with this problem

Answer 1

Answer is 41 ft

Explanation:

From the right angled triangle above, two sides are known. That is the adjacent and opposite. The hypotenuse is not known so we represent it with a variable say h

Using Pythagora's theorem we have,

`{h}^(2) = {12}^(2) + {12}^(2) \\ {h}^(2) = 144 + 144 \\ {h}^(2) = 288 \\ h = √(288) \\ h = 12 √(2)`

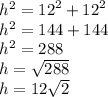
Having found the value of the third side, the perimeter of the triangle can now be determined by summing up the length of all the sides.

`perimeter = adjacent + opposite + hypotenuse \\ p = 12 + 12 + 12 √(2) \\ p = 24 + 12 √(2) \\ p = 40.97 \\ to \: the \: nearest \: whole \: number \\ p = 41 \: ft`

Therefore the perimeter of the triangle is 41 ft.