Answer:
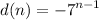
Explanation:
Since the sequence above is a geometric sequence
For an nth term in a geometric sequence
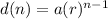
where
a is the first term
r is the common ratio
n is the nth term
To find the common ratio divide the previous term by the next term
That's
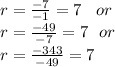
So the common ratio / r = 7
the first term is - 1
Substitute the values into the above formula
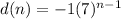
We have the final answer as
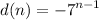
Hope this helps you