Answer:
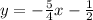
Explanation:
Slope-intercept form: y= mx +c, where m is the slope and c is the y-intercept.
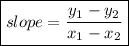
Slope
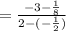
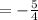
Substitute the value of m into the equation:
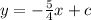
To find the value of c, substitute a pair of coordinates the line passes through into the equation.
When x= 2, y= -3,
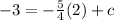
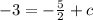
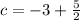
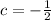
Thus, the equation of the line is
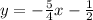 .
.