Answer: (x - 2)² + (y - 3)² = 25
Explanation:
The equation of a circle is: (x - h)² + (y - k)² = r² where
- (h, k) is the center of the circle
- "r" is the radius of the circle
We are given three coordinates. Input those as (x, y) into the circle equation. This creates a system of equations with 3 equations and 3 unknowns (h, k, r).
EQ1: (5 - h)² + (7 - k)² = r²
EQ2: (-1 - h)² + (7 - k)² = r²
EQ3: (5 - h)² + (-1 - k)² = r²
Evaluate EQ1 & EQ2:
(5 - h)² + (7 - k)² = r²
-[ (-1 - h)² + (7 - k)² = r² ]
(5 - h)² - (-1 - h)² = 0
(5 - h)² = (-1 - h)²

5 - h = ±(-1 - h)
5 - h = -1 - h 5 - h = -(-1 - h)
6 ≠ 0 5 - h = 1 + h
Disregard 4 = 2h
2 = h
Input h = 2 into EQ2 & EQ3 and evaluate:
(-1 - 2)² + (7 - k)² = r² --> 9 + (7 - k)² = r²
(5 - 2)² + (-1 - k)² = r² --> - [ 9 + (-1 - k)² = r² ]
(7 - k)² - (-1 - k)² = 0
(7 - k)² = (-1 - k)²
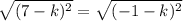
7 - k = ±(-1 - k)
7 - k = -1 - k 7 - k = -(-1 - k)
8 ≠ 0 7 - k = 1 + k
Disregard 6 = 2k
3 = k
Input h = 2 and k = 3 into any of the equations to solve for r²:
EQ1: (5 - 2)² + (7 - 3)² = r²
9 + 16 = r²
25 = r²
Input h = 2, k = 3, and r² = 25 into the equation of a circle:
(x - h)² + (y - k)² = r²
(x - 2)² + (y - 3)² = 25