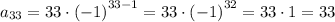11)
5, -5, -15, -25, ...
-5-5 = -10; -15-(-5) = -10; -25-(-15) = -10 ⇒ this is an example of arithmetic sequence that has explicit patern (evey next term is 10 less than previous one)
difference: d = -10
first term: a = 5
so the formula:
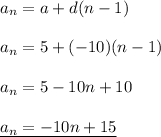
and:
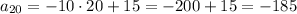
12)
19, 26, 33, 40, ...
26-19 = 7; 33-26 = 7; 40-33 = 7 ⇒ this is an example of arithmetic sequence that has explicit patern (evey next term is 7 more than previous one)
difference: d = 7
first term: a = 19
so the formula:
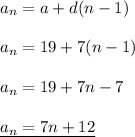
and:
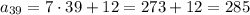
13)
-20, -29, -38, -47, ...
-29-(-20) = -9; -38-(-28) = -9; -47-(-38) = -9 ⇒ this is an example of arithmetic sequence that has explicit patern (evey next term is 9 less than previous one)
difference: d = -9
first term: a = -20
so the formula:
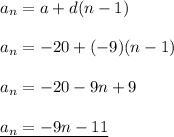
and:

11)
1, -2, 3, -4, ...
-5-1 = -3; 3-(-2) = 5 ≠ -3 ⇒ this is NOT an example of arithmetic sequence
however it has explicit patern:

so: